A Step-by-Step Guide to the Desmos SAT Calculator

Since March 2024, the Desmos calculator is integrated directly into the SAT’s test-taking software for every student taking the Digital SAT. And I have to wonder, what were they thinking? The Desmos graphing calculator is absurdly powerful, and, though it won’t help you solve every problem on the test, it can often break 15–20 problems across the two math modules. 

Most importantly, using it is fast, brain-dead, and accurate. On a test where the score is all that matters, we LOVE that. So in this article, I will show what types of SAT Math problems you can use the Desmos SAT calculator to solve, and I’d encourage you to try these methods, even if you know how to solve the problem traditionally. I put even my best SAT students through a rigorous Desmos crash course so they can blaze through those problems and save brainpower for the harder stuff. 

What is the Desmos SAT Calculator?

The Desmos SAT Calculator is a built-in, online graphing calculator available on the digital SAT. It allows students to perform complex calculations, graph equations, analyze functions, and visualize mathematical concepts directly within the test interface. Since it’s integrated into the exam, students don’t need to bring a physical calculator, making it a convenient and powerful tool for tackling math problems efficiently.

What Types of Problems Should You Use Desmos SAT Calculator to Solve?

Desmos can’t be used for every type of problem on the SAT, but it will solve a lot of them. Here is a list of the types of problems you should strongly consider solving with the Desmos calculator and a list of problems that are sometimes worth solving without the Desmos calculator.

Types of Problems You Should Solve Using the Desmos SAT Calculator

1. Solving Single Variable Equations
2. Evaluate the Function at X
3. Number of Solutions
4. Solving Systems of Equations
5. Solving Systems of Inequalities
6. Finding the Equation of a Line from Points
7. Finding the Equation of a Non-Linear Function from Points
8. Finding an X or Y-Intercept from an Equation
9. Finding the Vertex (Minimum/Maximum) of a Quadratic
10. Transformation of a Function
11. Finding Points on a Circle
12. Finding Mean and Median of a List of Numbers

Problems You Can Solve Using the Desmos SAT Calculator

The “maybe” category of problems usually means that it takes too long to type them into Desmos or that it requires lots of small adjustments to get to the answers.

1. Equivalent Expressions
2. Intersecting with a Quadratic at 1 Point
3. Intersecting with a Quadratic at 0 Points

Examples of Problem Types You Should Use the Desmos SAT Calculator to Solve

Next, I will give you examples of every type of problem mentioned here with step-by-step instructions on what to type into the Desmos calculator. You can access an online version of the calculator here, and it is functionally identical to the one used on the exam.

1. Solving Single Variable Equations

Desmos steps:

1. In line 1, type p^2 + 2p -27 = -2p + 50.
2. Scroll out on your graph if you don’t see anything right away. You should see vertical lines. The x-values of the vertical lines are the solutions to the equation.

2. Evaluate f(x) at x=?

Variation 1:

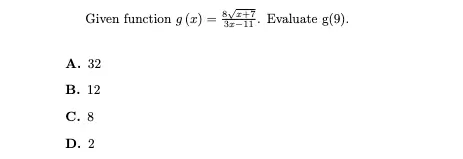
Desmos steps:

1. In line 1, type g(x) = 8sqrt(x+7) / (3x-11).
2. In line 2, type g(9).
3. The answer will be displayed in the lower right corner of line 2.

Variation 2: 

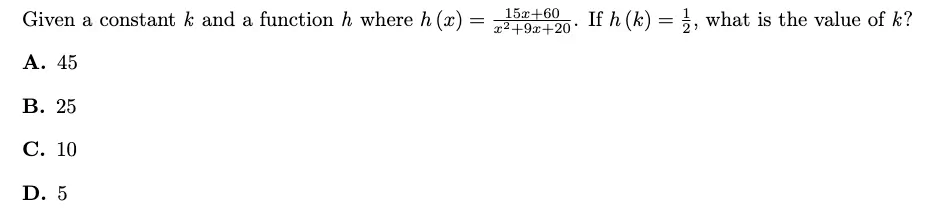
Desmos steps:

1. In line 1, type h(x) = (15x + 60)/(x^2 + 9x + 20).
2. In line 2, type h(x) = 1/2.
3. The answer is the x-value of the point where they intersect.

Challenge: Here is a harder version of variation 1. Just type multiple f(#) lines for each of the x-values in the table.

3. Number of Solutions

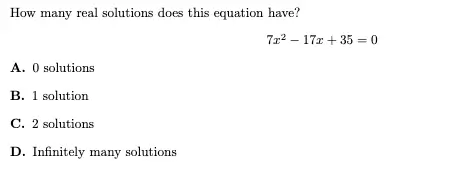
Desmos steps:

1. In line 1, type f(x) = 7x^2 – 17x + 35 (the left side of the equation)
2. In line 2, type g(x) = 0 (the right side of the equation)
3. Count how many places they intersect.

Note: If you are worried about the “infinitely many” case, click the icon near the line number to hide on of the function. If they are on top of each other then it is infinitely many solutions.

4. Solving Systems of Equations

This is one of the best uses of Desmos.

Desmos Steps:

1. In line 1, type 3y + 13 = -7x.
2. In line 2, type -2x + 5y = 70.
3. The answer will be the point where these two graphs intersect. The point should be automatically highlighted by Desmos. Here, it wants the y-value of that point.

5. Solving Systems of Inequalities

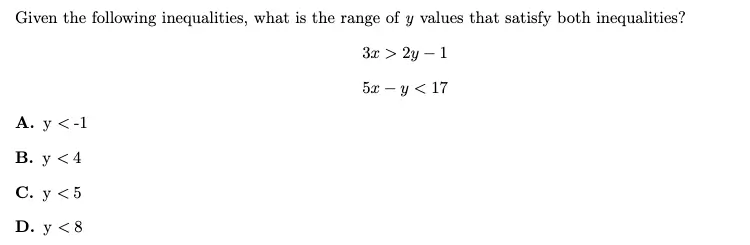
Desmos steps:

1. In line 1, type 3x > 2y – 1.
2. In line 2, type 5x – y < 17.
3. In the graph, find the lowest point where the two shaded areas overlap. The answer will be y < # where the number is the y-value of that point (or greater than, if going in the other direction).

6. Finding the Equation of a Line from Points

Desmos steps:

1. In line 1, type table. A table will pop up.
2. In the x₁ column, type your x-values from your points. In the y₁ column, type the corresponding y-values.
3. Under the line number (under the 1 on the left), hit the symbol the looks like a diagonal line between 4 dots. 
4. Your answer is under EQUATION.

Another version of this problem for you to try:

Hint: Can we re-write the solutions as points?

7. Finding the Equation of a Non-Linear Function from Points

Desmos steps:

1. In line 1, type table. A table will pop up.
2. In the x₁ column, type your x-values from your points. In the y₁ column, type the corresponding y-values.
3. Under the line number (under the 1 on the left), hit the symbol that looks like a diagonal line between 4 dots. 
4. Click the dropdown which says Linear Equation and select from the menu the type of equation you are trying to model. Here that would be Exponential Regression. You may also need to use the Quadratic or Cubic Regressions on the SAT.
5. Your answer is under EQUATION.

8. Finding an X or Y-Intercept from an Equation

Desmos steps: 

1. In line 1, type in 7x/5 – 18 = 3y/4.
2. If you hover over your line, Desmos will highlight the y-intercept (and x-intercept(s)) automatically. The answer is the y-value of that point.

9. Finding the Vertex (Minimum or Maximum) of an Equation

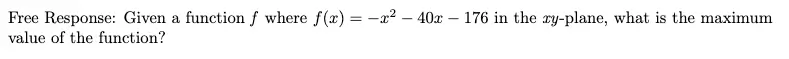
Desmos steps:

1. In line 1, type in f(x) = -x^2 – 40x – 176.
2. If you hover over your line, Desmos will highlight the maximum (or minimum) point automatically. The answer is the y-value of that point.

10. Transformation of a Function

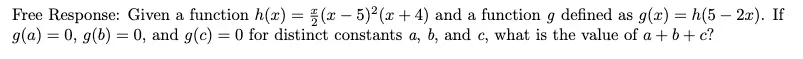
Desmos steps:

1. In line 1, type h(x) = x/2(x – 5)^2(x + 4).
2. In line 2, type h(5 – 2x). This will give you a transformed graph of the original function. The value of g(x) is 0 at its x-intercepts, which will be marked automatically. You could also type another equation f(x) = {insert what you need g(x) to equal} and look at the intersection points.

Note: Desmos will handle all the standard transformations. Try typing 7h(x), -g(h + 7), and h(2x) – 8. It will do them all.

11. Finding a Point on a Circle

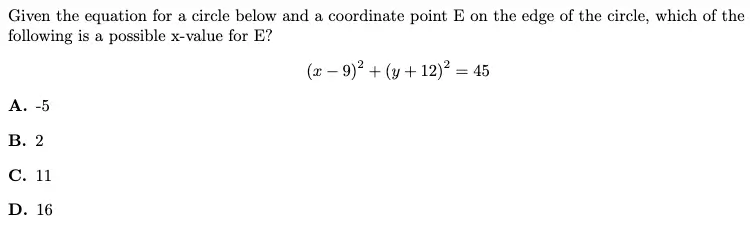
Desmos steps:

1. In line 1, type (x – 9)^2 + (y + 12)^2 = 45.
2. Your answer choices are x-values. Only one of them will match up with the x-values of the points on the circle.

12. Finding Median and Mean of a List of Numbers

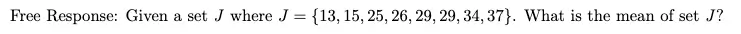
Desmos steps:

1. In line 1, type mean( ). For median, type median( ).
2. Put your list of numbers in the parentheses, separated by commas. Mean (13, 15, 25, 26, 29, 29, 34, 37). The answer will show up instantly.

Problems You Can Maybe Use Desmos to Solve

Generally, I advise that you avoid using Desmos for these if you can solve them traditionally, but Desmos will work in a pinch. Desmos can also be the best strategy for some of these if the problems are multiple-choice.

1. Equivalent Expressions

You can use Desmos to solve these, but it is very slow since you cannot copy and paste the equations. I recommend you only use Desmos if you cannot solve it by hand. 

Desmos steps:

1. In line 1, type table. A table will pop up.
2. In the header row, type x in the first box, 2(3x^2 – 4) – (x + 3)^2 in the second box, and each of your answers in the next 4 boxes.
3. Type a bunch of random x-values (numbers) in the first column. The answer choice with answers that match the ones is the second column will be the answer. 

2. Intersecting with a Quadratic at 1 Point

You can do this problem with Desmos, but it is finicky. In general, if it is free response and you know how to do it by using the discriminant, I would do that. If it is multiple choice or you can’t remember how to do the traditional method, then maybe use Desmos.

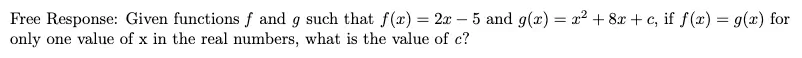
Desmos steps:

1. In line 1, type f(x) = 2x – 5/2.
2. In line 2, type g(x) = x^2 + 8x + a. (For constants, I typically stick to a and b in Desmos. For variables, I usually stick to x and y.)
3. You should see an option pop up to add a slider for a. Click the blue box to do that.
4. Slide the slider back and forth until you can get the lines to only meet at one point. If you need to extend the range of the slider (default is -10 to 10), you can click on the numbers at the end of the range to type your own custom values. If you are working on a multiple-choice question, you can click on the number after a = to input each of your answer choices.
5. Once you get them to line up at one point, that value of a is the answer.

3. Intersecting with a Quadratic at 0 Points

This problem is almost, but not quite, a classic intersection problem. It is effectively asking what values of d make g(x) = 3x^2 − 24x + d and h(x) = 0 not intersect. Like the previous problem type, I would generally use the discriminant rule instead if it is a free response question, but it can be done in Desmos. If it is a multiple-choice problem, Desmos is a fine option.

Desmos steps:

1. In line 1, type g(x) = 3x^2 – 24x + a.
2. In line 2, type h(x) = 0.
3. Add a slider for a by clicking the box in the line 1.
4. Start typing in values for c until you get the two lines to intersect at 1 point. Beyond that value for a they will not intersect, so that will be your answer. If it is multiple-choice, then the value for a which gives no solutions is the one where the lines do not intersect at all.

Problems You Should NOT Use Desmos to Solve

There are also several problems that are related to Desmos-able problem types that you should avoid solving with Desmos.

Problems to Avoid

• System of Linear Equations with a Constant (Parallel Lines)
• Any Other Parallel Problems
• Difficult Mean & Median Problems
• Finding Center or Radius of a Circle
• Last 4 Problems of Module 2 (unless you very obviously can use it, it’s a trap)

I want to particularly highlight that first one, since Desmos is usually so powerful for solving systems of equations.

Here’s an example so you can see how to identify these problems.

Example of System of Linear Equations with a Constant

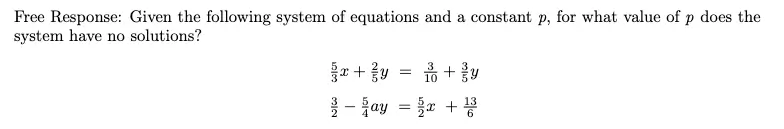
This problem looks like the other systems of equations problems where we definitely want to use Desmos, but it is not. You can tell this is a linear system of equations because the x in both equations is only to the power of 1 (x¹). If you see this, you need to solve for the slopes of these equations and set them equal to each other because these equations are parallel lines. Do NOT use Demos with constant slider for this. It is too inaccurate.

Conclusion

The Desmos SAT calculator is a very powerful tool you have at your disposal for the SAT Math section, but the key to mastering it is building your skill at identifying the problems you can use it on. As always, the best way to get better is to use it while working through practice problems.  

And now YOU are ready to start breaking the SAT Math problems with the DESMOS calculator. Remember always ask yourself, “Can I cheese this with DESMOS?” Your brain and your test core will thank you. Happy testing!